A Beginner Guide to Learn Dynamic Programming and Become a Pro

Technology has developed leaps and bounds over the past decade. Now everywhere we look we are surrounded by it. It is embedded so deep and intertwined with our lives so closely, that we cannot imagine our lives from without it. From AI tools making our presentation to self driven cars, our world has is incomplete without it. One such fascinating program that we will learn about is dynamic programming.

In this blog, you will learn when to use this program, its approaches and algorithms, and how you will use this program to solve problems. Moreover, you will see the difference between this program and recursion, along with some examples. So, let us begin with the meaning of the term.

What is Dynamic Programming(DP)? | A Brief

Dynamic programming(DP) is a computer science programming procedure where an algorithm problem is broken down into smaller parts, the parts are saved, and then the sub parts are optimized to find the overall solution. It is usually done to find the maximum and minimum range of the algorithm query.

The person who came up with this concept of DP in 1950s was Richard Bellman. This technique is used for mathematical optimization and also a computer program. It applies to problems that can be broken down into overlapping sub-parts or optimum substructures.

When you break a complex problem into small groups, the overlapping problems are equations that reuse those smaller problems equations several times to arrive at a solution.

Whereas, optimum substructures locate the best solution of the problem, then build solutions that provides the best results in totality. The results are then stored in a table to be reused when the same problem arises in the future.

When to Use Dynamic Programming

You saw in the previous section what is dynamic programming, now, we will witness when to use dynamic programming. It will furnish you with a clear framework from which you can learn when to use this program. So, let us look at it in detail.

• Overlapping Sub-problems

Dynamic programming flourishes in solving overlapping sub-problems. These are smaller parts within a bigger problem. Moreover, they are solved independently and repeatedly. Later, these solutions are stored to prevent redundant work and speed up the entire process.

For example: The travel route from city A to B has many options. So, instead of calculating the distance every time, you map out different routes and later store the distance and reuse it whenever you require.

• Optimal Substructure 

Under this concept, you will reach an optimal solution to a bigger problem by developing optimal solutions to smaller sub-problems. This process permits us to break down bigger problems into smaller parts and solve them step-by-step.

For example: Lets go back to the previous example and let say you have found the shortest route from city A to B and similarly the route from city B to C. The shortest route from City A to C through City B can combine those two shortest routes.

So, now yo know when you can use dynamic programming technique. As it being a computer science division, if you have issues regarding this method, you can take computer science assignment help.

Approaches of Dynamic Programming

Now lets move on to the next section in the blog which will enlighten you about the different approaches of dynamic programming(DP). DP uses two primary approaches to solve problems. The first one is top-down approach also known as "memoisation" and the second is the bottom-up approach also known as "tabulation". Lets study these approaches in detail.

• Top-Down (DP) Approach

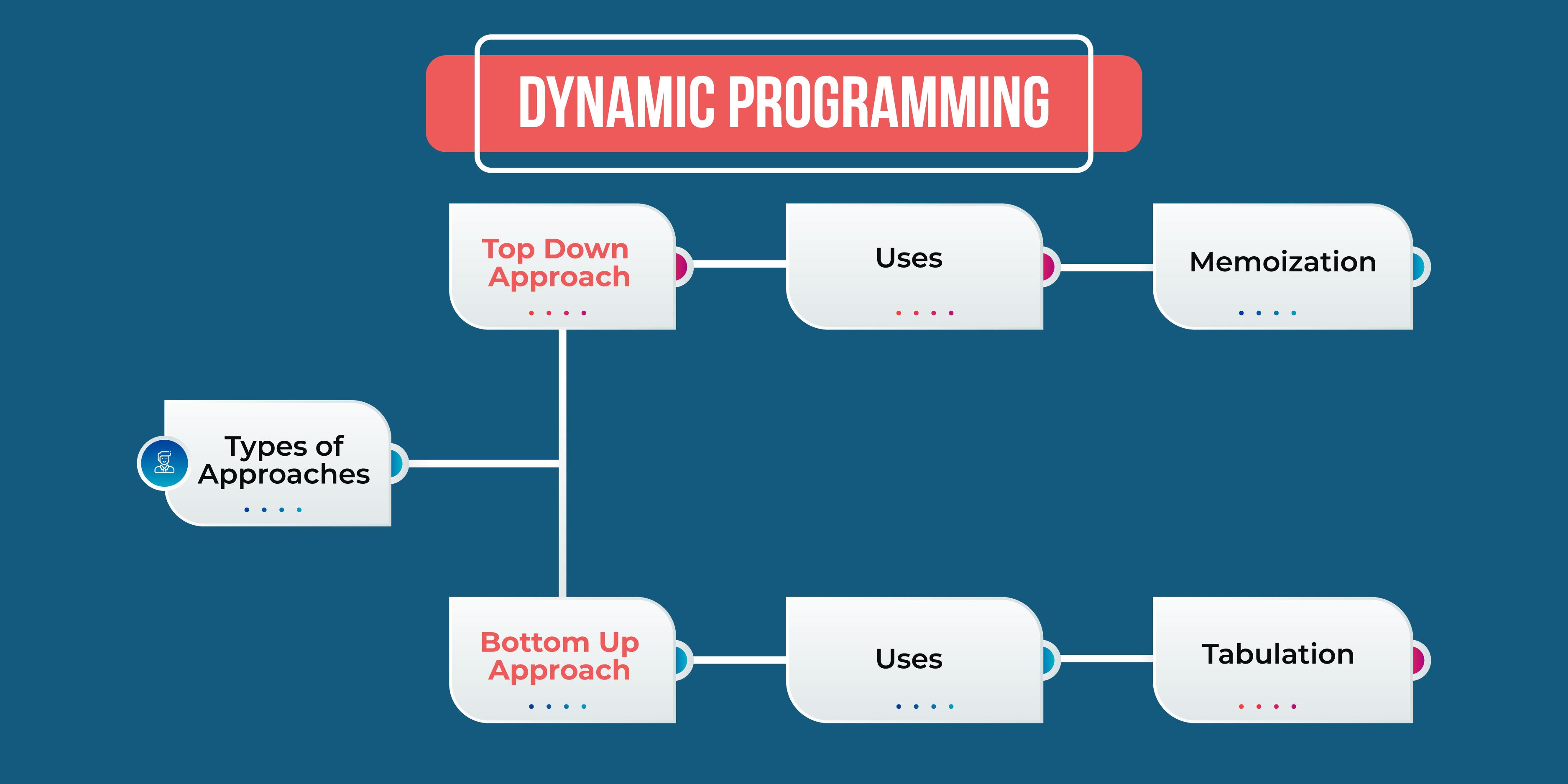
In the top-down approach, you begin with the original problem and break it into sub-problems. Think of it as starting at the top of the pyramid and working your way down.

You break the issue into smaller parts and store there answers to be reused when needed. As you go bigger problems becomes small and less complicated and the solutions are stored in a data structure like dictionary or array to avoid wasting time in the future. This process is equivalent to adding the recursion and caching steps.

Key Points:

• Easy to Understand and Apply
  
  a) This approach breaks problems into smaller parts and makes it easy to figure out what needs to be done
  b) Each step solves a smaller sub-problem and makes it more manageable and reusable for similar issues.

• On-Demand Sub Problem Solving
  
  a) This approach stores solutions to sub-problems and allows users to reuse them when needed.
  b) This flexible approach helps to address specific parts of an issue without recomputing everything. 

• Debugging Positives 
  
  a) Breaking problems into smaller parts simplifies debugging. It helps you to solve problems easily.

 However, this approach leads to storing more memory in the call stack that can result in reduction in the overall performance and stack overflow. 

• Bottom-Up (DP) Approach

This approach which is also known as tabulation takes into the opposite direction. This method solves issues by breaking them into smaller parts and solving them with the smallest mathematical value and then working to the top of the pyramid. The solutions to the sub-problems are compiled in a manner that they fall and loop back on itself.

 Here we fill up a table in a manner that uses the previously filled value in the table. This way when we come to solve the bigger problem we already have the solutions to the sub-problems. 

Key Points

• Solving Sub Problems
  
  a) In this approach, you solve smaller sub-problems first before tackling big ones.
  b) When you breakdown problem into smaller parts, it becomes manageable and you build a base to solve bigger problem. 

• Recursion Removal
  
  a) The bottom-up approach avoids recursion altogether.
  b) It removes the worry of stack overflow and reduces overhead from recursive function calls.

• Memory Efficient

            a) The absence of recursion allows for effective memory use
            b) You do not need to maintain a call stack which lead to better memory management.

• Time Complexity Reduction

            a) Recalculating the same values in recursion consumes a lot of time.
            b) This approach solves sub-problems directly, which results in improved time complexity.

So, this is how top down vs. bottom up Dynamic Programming approaches works. If you have issues and are still skeptical about how to use dynamic programming, you can seek programming assignment help.

Algorithms of Dynamic Programming 

You have reached halfway and have seen the definition, approaches and when to use dynamic programming. Now, we will see the dynamic programming algorithms and how it is used to solve problems. So, without wasting any time lets get down to it.

• Floyd-Warshall Algorithm

 This method use a procedure of DP to locate the shortest routes. Moreover, it find out the quickest way across all pairing of vertices in a graph with weights. You can use both direct and indirect weighted graphs.

 This program compares each pair of vertices' potential routes through the graph. It slowly optimizes the shortest pathway between two vertices in a chart. This method of DP contains two sub-types:

      1. Behaviour with Negative Cycles

You use this algorithm to find negative cycles. You do it by checking diagonal path matric for a negative number which would show the graph containing one negative cycle. In it the sum of the edges is a negative value and cannot have a shortest route between any pairs of vertices.

       2. Time Complexity

This algorithm has three loops, each with regular complexity. As an end result, it has the time complexity of O(n3). Where, n denotes the numeral of network nodes.

       3. Bellman Ford Algorithm

This algorithm finds the shortest pathway from a particular source vertex to every other weighted digraph vertices. Moreover, this algorithm can handle graphs that have some edges of the graph in negative numbers but produce a correct answer.

This algorithm works by relaxation. It means it give approximate distance that continuously replaces until a solution is reached. This distances are generally overestimated in comparison to the distance between the vertices. The replacement values the minimum old value and the length of the new found route.    

• Greedy Algorithm

 Greedy algorithms are also used as optimization tools. This technique solves a problem by looking for an optimum solution to the sub-problems and later combining findings to get the most optimal answer.

 When this algorithm solve problems, it looks for a local optimum solution to search a global optimum. They guess what looks like optimum at the time; however, it does not assure a globally optimum solution.

 So, these are the three dynamic programming algorithms that solve a particular problem and reach a solution.

Stuck with Dynamic Programming Assignment

Hire Our Experts Writers for and Get Completely Original Document

Contact Us Now

The Signs of Dynamic Programming Suitability

In this section, you will see how you can identify whether a problem is suitable for solving dynamic programming. The common signs that show an issue might be solvable by dynamic programming are: 

• Overlapping Sub-problems:A problem you can break into smaller sub-problems ans solve them independently and you encounter same problem many time. 

• Optimal Substructure:A problem that depicts optimal substructure. It means you construe optimal solutions for a larger problem through optimal solutions to smaller ones.

• Recursive Nature:A problem you can express using recursion.

• Memoization Possibilities:If you can solve a recursive algorithm by memozing intermediate results.

• Sequential Dependencies:A problem whose solution depends on the previous results or stages, such as strings, graphs, and arrays. 

• Optimization or Counting:You can apply dynamic programming to maximize or minimize a value or counting problems.

• Recursive Backtracking Inefficient:If you find a recursive reversal algorithm that is slow due to repeated calculation.

• Sub-problem Independence:Problems that have sub-problems but are entirely independent of each other. 

• Limited Set of Options:Problems where the options are limited and do not grow rapidly.

 All these are the characteristics of problems that can be solved through dynamic programming. If you have issues understanding this concept you can seek assignment writing service.

Steps to Solve Problems of Dynamic Programming

This faction of the blog will give you information about the steps you must take to solve problems by applying dynamic programming. So, lets see what those steps are.

1. Define Problems and Its Sub-problems

The first thing you must do is to understand the problem carefully. Then, locate the primary problem and divide them into smaller, overlapping sub-problems. Clearly define the sub-problems on which you can build your solution. It must have a sub-structure.

2. Express the Sub-problem As a Mathematical Recurrence

 Once you have located the sub-problems, assign them mathematical recurrence or recursive equations. This equation will define how to build a solution to a given sub-problem by using solutions to smaller sub-problems.

 The recurrence should be constructed in a way that relates to one or more smaller sub-problems.

3. Define the Strategy for Memoising the Array

You must decide what approach you will use to store and retrieve solutions to sub-problems. If you use memoisation, you must create a data structure to cache or retrieve the solutions. Dynamic programming Python often comes with built-in libraries that are fit for memoisation. Moreover, define the memoisation structure. The dimensions of the array will rely on the range of sub-problems that you need to solve.

4. Code the Solution

Now, you use the DP solution utilizing the chosen approach. You will do it on the basis of mathematical recurrence and memoisation strategy. Moreover, you will begin with smaller problems and build your way to the main problem. Compute and store the solutions to each sub-problem in your array.

You must ensure that your code handles boundary cases, base cases, and termination conditions. Lastly, the value stored in the primary problem cell will be the optimal solution to the main problem.

Let us understand it with the help of the Fibonacci Series

• Identify Sub-problems:Divide the main problem into smaller independent sub-problems. For example: F(n-1) and F(n-2) 

• Store solutions:You must solve each sub-problem and store the solution in a table or array. 

• Build-Up Solutions:You will use the stored solutions to build up the solution to the primary problem. For F(N), glance up F(N-1) and F(N-2) in the format and add them.

• Avoid Re-computation: When you store solutions, you ensure that each sub-problem is solved only once, for example, F(2).

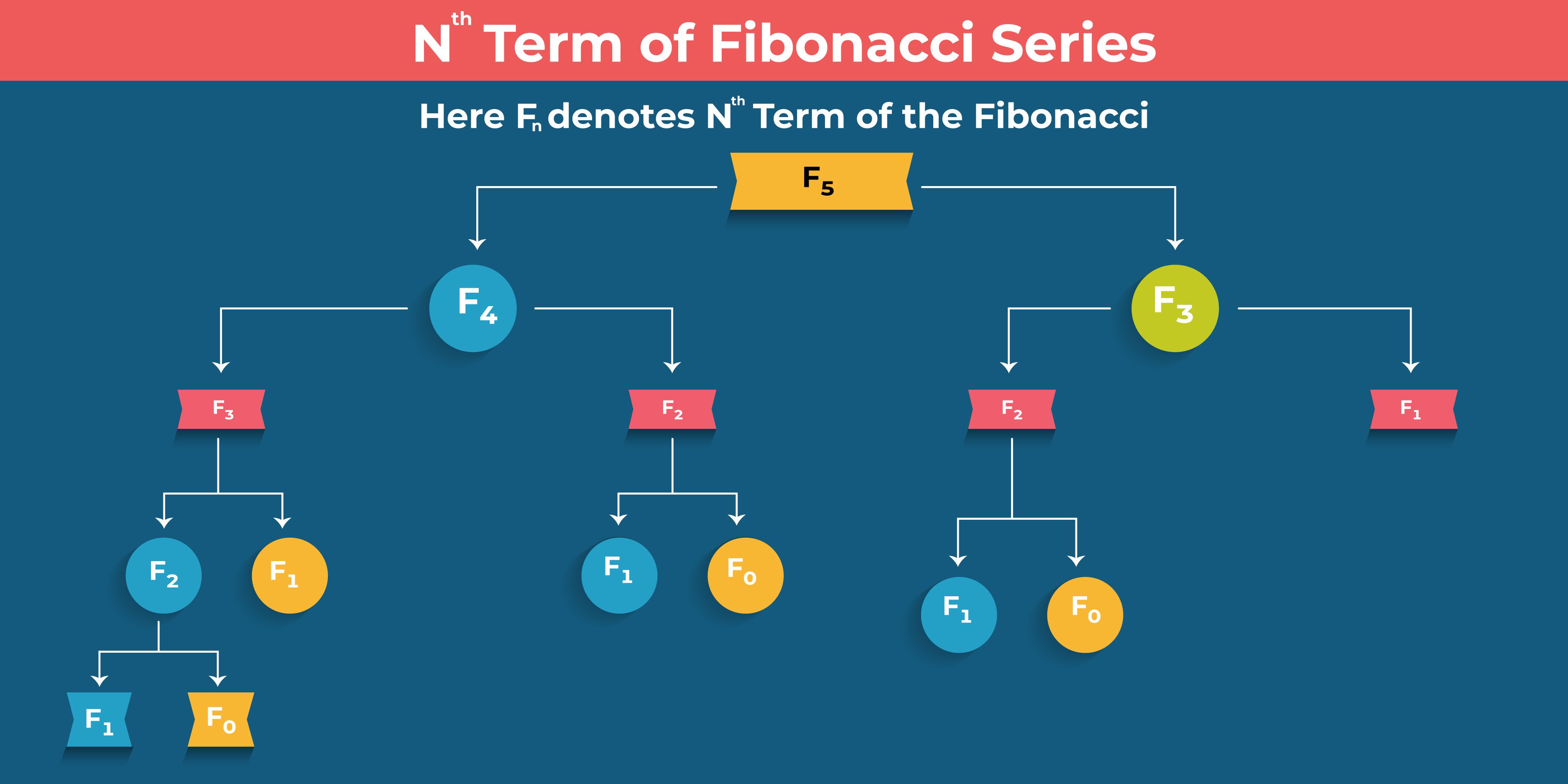
 So, you saw how to solve a problem using dynamic programming techniques. You can use any approach that suits your problem and reach solutions. 

Difference Between Dynamic Programming & Recursion

 This section will explain the differences between dynamic programming and recursion. Let's examine the salient points of distinction between the two.

Recursion is a vital concept of computer science in which the solutions to a problem entirely hinge on the solutions to its smaller sub-problems. 

Dynamic programming is an optimization approach for recursive answers. It is used when solving recursive functions that make repeated calls to the same inputs.

However, not all problems utilizing recursion can be solved by dynamic programming. Only the solutions that overlap, a recursion solution, can be achieved by using the divide-and-conquer method.

For instance, Problems like merger, quick sort, and sort are not considered dynamic programming problems. This is the detailed difference between dynamic programming and recursion. If you have any issues, you can seek help from experts.

Advantages of Dynamic Programming

You will now see the advantages of dynamic programming in detail in this section. So, lets have a look. 

• Optimization- This program is primarily used to optimize problems where the end goal is to search for a solutions among a set of possible solutions. 

• Efficiency- This program reduces obsolete computations by storing, reusing and overlapping sub-problems.

• Clarity and Structure- This program also presents a structured and arranged approach to cracking problems. It breaks down issues into smaller and more effortless sub-problems, which provides clarity.

• Versatility- This program is quite adaptable and can be used to solve many issues. It can be used in sequence alignment and shortest path algorithms.

• Accuracy-This program also ensures accuracy in solutions. It considers all possible sub-problems and exhausts all paths to find the optimal solution.

• Reusability-This program also pushes for the reuse of codes and solutions. Once an issue is solved, it can be stored and reused.

• Deterministic- This program also ensures it produces the same optimal findings for a given set of inputs.

• Real-World Applications- This program is not only theoretical but also has practical applications in various fields, such as economics, AI, and computer graphics.

• Educational Value- This program also helps you develop problem-solving skills and algorithmic thinking.   

All these are the plus points of dynamic programming. Learning this program will help you immensely in the field of computer science.

Trouble Understanding Dynamic Programming?

Hire our Learn the Basics and When to Use Dynamic Programming Approaches

Ask Our Experts

Dynamic Programming: Examples

You have come a long way and have seen definitions, when to use them, approaches, and dynamic programming algorithms. Now, in this faction, you will witness some samples related to dynamic programming. So, let's peek at them and try to comprehend them more apparently.      

1. Python Problem 

The Python principle represents a position Fibonacci (n), which aids in estimating the nth Fibonacci numeral. Here is the analysis:

def fibonacci(n):

fib = [0]* (n + 1)

fib[0] = 0

fib[1] = 1

for i in scope(2, n + 1):

fib[I] = fib[I-1] + fib[I-2]

return fib[n]

Explanation 

• Initialization: 

Definition Fibonacci (n)- It explains a function named Fibonacci that takes on an integer n as input, which represents the desired Fibonacci number's place or position in the sequence.

 fib= [0]*(n+1) creates a list that is called fib of size n+1, initialized with zeros. This list will store all the Fibonacci numbers.

 fib[0]=0 and fib[1]=1 sets the primary two numbers in the list, as the sequence starts with 0an 1. 

• Iteration:

 For i in scope (2, n+1): circles from 2 up to n

 fib[i]= fib[i-1]+ fib[i-2] it computes the ith Fibonacci number by counting the prior two Fibonacci numbers stowed in the list and then assigns the finding to the present place i in the list.

• Return Value:

 Return fib returns the nth Fibonacci number stored at index n in the fib list.

2. Knapsack Problem 

def knapsack(W, WT, VAL, N):

DP = [[0] * (w+1) for _ in scope(N+1)]

for I in Scope(1, N+1):

for W in Scope(1, W+1):

if wt[i-1] <= w:

DP[I][W] = MAX(VAL[I-1] + DP[I-1][W-WT[I-1]], DP[I-1][w])

else:

dp[I][W] = DP[I-1][W]

return dp[n][W]

This is a traditional model of optimization that concerns exploring the optimal subset of things to load in a knapsack with a finite ability so as to maximize the worth of the things packed. Moreover, this problem can also be decoded by using dynamic programming, splitting it down into smaller sub-problems and cracking each one only once.

 You saw the dynamic programming examples. We hope you understand them. If you want more clarification, you can search the web and ask, "Can anyone do my assignment?"

Seek Experts Assistance with Dynamic Programming

We hope you were able to understand the basics of dynamic programming. All these sub-headings will help you to understand this technique without much discomfort. Our experts at Assignment Desk can also help you learn the fundamentals and apply them to real-life problems.

You can also ask our experts to prepare a document on this subject, and you can rest easy knowing that your paper will contain all the vital information about dynamic programming.